The numerical integration library named “SciPy” gives varied instruments and strategies for fixing several types of integrals. The “scipy.combine.tplquad()” technique of the “scipy” library is used to compute a triple (particular) integral of a operate of three variables over a given area.
This Python put up presents an in depth information on the “scipy.combine.tplquad()” technique by overlaying the below-given contents:
What’s the “scipy.combine.tplquad()” Technique in Python?
The “scipy.combine.tplquad()” technique is used to carry out triple integration over a specified vary of variables. It makes use of an adaptive algorithm to numerically consider the integral and gives correct outcomes even for complicated features and areas.
Syntax
scipy.combine.tplquad(func, a, b, gfun, hfun, qfun)
Parameters
Within the above syntax:
- The “func” parameter specifies the operate to be built-in via the outlined area.
- The “a” parameter specifies the decrease restrict of integration alongside the “x”-axis.
- The “b” parameter specifies the higher restrict of integration alongside the “x”-axis.
- The “gfun” parameter signifies the decrease restrict of integration alongside the “y”-axis. It may be a operate or fixed worth.
- The “hfun” parameter signifies the higher restrict of integration alongside the “y”-axis. It may be a operate or fixed worth.
- The “qfun” parameter defines the decrease and higher limits of integration alongside the “z”-axis.
Return Worth
The return worth of the “scipy.combine.tplquad()” technique is a tuple of two values:
- The primary floating worth is the operate “func” triple integral.
- The second floating worth is an estimate of the integral error.
Instance 1: Calculating Triple Integral of Perform Utilizing the “scipy.combine.tplquad()” Technique
Let’s say we need to decide the triple integral of the under operate:
f(x, y, z) = x^3 + y^3 + z^3
The area outlined for the above operate is, as follows:
x ∈ [0, 1], y ∈ [0, 2], and z ∈ [0, 3].
Right here’s the code that computes the triple integral of the above operate with the outlined area:
def f(x, y, z):
return x**3 + y**3 + z**3
outcome = scipy.combine.tplquad(f, 0, 1, lambda x: 0, lambda x: 2, lambda x, y: 0, lambda x, y: 3)
print(“Outcome:”, outcome[0])
Within the above code:
- The “scipy.combine” module is imported.
- The user-defined operate “f(x, y,z)” defines the operate we need to combine.
- The “scipy.combine.tplquad()” technique is used to guage the triple integral.
- The “0” and “1” parameters are used to specify the decrease and higher limits of integration alongside the “x” axis.
- The lambda features lambda “x: 0” and lambda “x: 2” outline the bounds of integration for “y”-axis.
- The lambda features lambda” x, y: 0” and lambda “x, y: 3” outline the bounds of integration for “z”-axis.
- Lastly, print the results of the triple integration.
Output

The triple integration has been decided.
Instance 2: Calculating Triple Integral of Perform With Exponential Time period Utilizing the “scipy.combine.tplquad()” Technique
Let’s analyze the under code:
from math import exp
def f(z, y, x):
return x * y * z * exp(-x * y * z)
output = scipy.combine.tplquad(f, 0, 1, lambda x: 0, lambda x: 1, lambda x, y: 0, lambda x, y: 1)
print(output[0])
In these code traces, the triple integral of the enter operate having the exponential time period “exp(-x * y * z)” is calculated utilizing the “scipy.combine.tplquad()” technique. This technique mechanically makes use of a particular integration method to deal with the exponential time period.
Output
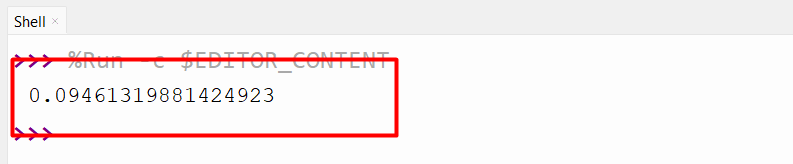
The triple integration has been computed appropriately.
Conclusion
The “scipy.combine.tplquad()” technique is used to carry out triple integration of easy to complicated features over a variety of variables in Python. This technique takes a number of parameters resembling operate, and decrease and higher limits for the “x” and “y” axis, and determines a triple integration. This text delivered a radical tutorial on the “scipy.combine.tplquad()” technique utilizing quite a few examples.