SciPy Linear Algebra

In arithmetic, linear algebra offers with the research of vector areas, matrices, linear equations, determinants, eigenvalues, and others. The “Scipy” library in Python gives a set of instruments and algorithms for scientific computing, such because the “scipy.linalg” module, which provides a wealthy set of capabilities and courses for linear algebra operations.

This weblog gives an in-depth tutorial on the Python “scipy.linalg” module utilizing the beneath content material:

What’s the “scipy.linalg” in Python?

The “scipy.linalg” module of the Python “scipy” library comprises varied linear algebra capabilities to carry out sure operations comparable to discovering matrix determinants, figuring out the matrix inverse, calculating the matrices norm, and so forth. Each NumPy and SciPy libraries share the performance of the “scipy.linalg” submodule.

Let’s begin with a “clear up()” perform of the “scipy.linalg” module to resolve the given linear equations:

Instance 1: Fixing Linear Equations Utilizing the “scipy.linalg.clear up()” Operate

This instance makes use of the “scipy.linalg.clear up()” perform of the “scipy.linalg” module to resolve this linear equation.

Right here is the code:

Within the above code:

• The “linalg” and the “Numpy” modules are imported.
• The “array()” perform takes the coefficient worth of the precise facet of all of the given equations as an argument and retrieves a Numpy array.
• The “array()” perform is used once more to create a Numpy array by taking the coefficient worth of the right-hand facet of the equation.
• The “linalg.clear up()” perform takes the enter arrays representing the coefficient worth of the precise and left-hand facet of the given linear equations and retrieves an answer array.

Output

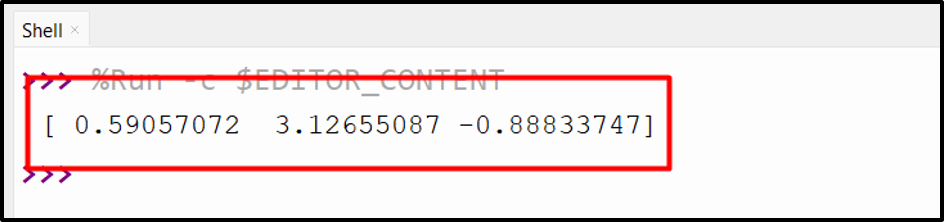
The linear equation has been solved.

Instance 2: Figuring out the Matrix Inverse Utilizing the “scipy.linalg.inv()”

On this instance, the “scipy.linalg.inv()” perform determines the matrix inverse:

Within the above code:

• The “linalg” and “numpy” modules are imported.
• The “array()” perform takes the equation worth and initializes it as a Numpy array.
• The “linalg.inv()” perform takes the array worth as an argument and retrieves an inverse array matrix.

Output

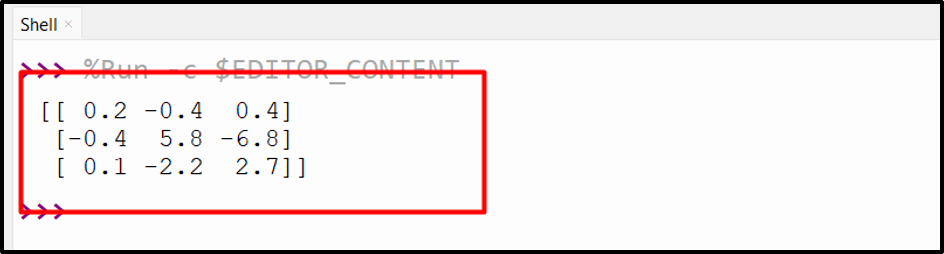
The inverse of the enter matrix has been decided.

Instance 3: Figuring out the Determinant Matrix Utilizing the “scipy.linalg.det()”

The “scipy.linalg.det()” perform takes the matrix and retrieves the determinant (Scalar Worth). Let’s overview this code:

Within the above code, the “numpy.array()” perform takes the matrix worth and creates a Numpy array. The “scipy.linalg.det()” perform takes the array (matrix) as an argument and retrieves the scalar worth.

Output

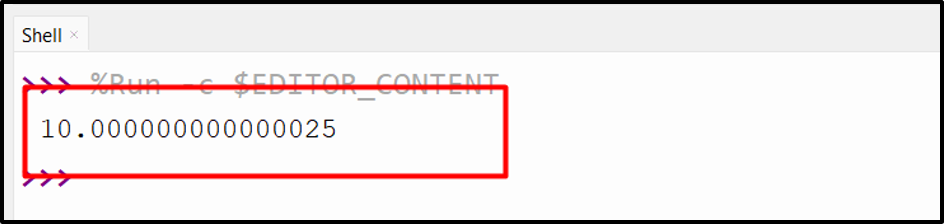
The determinant of the enter matrix has been decided efficiently.

Observe: You’ll be able to test this official documentation for all Python “scipy.linalg” module capabilities.

Instance 4: Figuring out the Norm of Matrices Utilizing the “scipy.linalg.norm()” Operate

This instance determines the norm or convergences of the sequence of matrices utilizing the “scipy.linalg.norm()” perform:

Within the above code:

• The 2 modules “linalg” and “numpy” are imported.
• The “array()” perform creates a Numpy array by taking two components as an argument.
• The “linalg.norm()” perform takes the array as an argument and returns the norm of the matrix, which is a measure of its size or measurement. By default, it makes use of the “2-norm”, calculated because the sq. root of the sq. sum of the weather.
• The “linalg.norm()” perform is used once more to retrieve the norm of a matrix with a unique worth of the parameter “ord”, which specifies the kind of norm to make use of. On this case, it makes use of the “1-norm”, calculated because the sum of absolutely the values of the weather.

Output

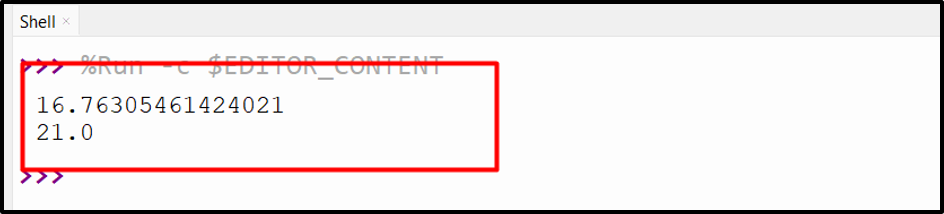
The norm worth has been calculated efficiently.

Conclusion

The “scipy.linalg” module of the “scipy” library gives varied capabilities comparable to “clear up()”, “det()”, “inv()”, “norm()”, and others to carry out an operation on linear algebra equations. The  “scipy.linalg.clear up()”, “scipy.linalg.det()”, and “scipy.linalg.inv()” capabilities are used to resolve the linear algebraic equation, decide the determinant and inverse of the enter matrix. This Python submit introduced just a few “scipy.linalg” module capabilities utilizing quite a few examples.